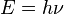Quantum mechanics

Quantum mechanics , also known as quantum physics or quantum theory , is a branch of physics providing a mathematical description of the wave–particle duality of matter and energy . Teori ini dikembangkan pada tahun 1925 oleh Werner Heisenberg . ^[1] Mekanika kuantum menggambarkan evolusi waktu dari sistem fisik melalui struktur matematika yang disebut fungsi gelombang . The theory was developed in 1925 by Werner Heisenberg . ^{[ 1 ]} Quantum mechanics describes the time evolution of physical systems via a mathematical structure called the wave function . Fungsi gelombang merangkum probabilitas bahwa sistem ini dapat ditemukan dalam keadaan tertentu pada waktu tertentu. The wave function encapsulates the probability that the system is to be found in a given state at a given time. Mekanika kuantum juga memungkinkan seseorang untuk menghitung efek pada sistem membuat pengukuran sifat-sifat sistem dengan mendefinisikan pengaruh dari pengukuran pada fungsi gelombang. Quantum mechanics also allows one to calculate the effect on the system of making measurements of properties of the system by defining the effect of those measurements on the wave function. Hal ini menyebabkan terkenal prinsip ketidakpastian serta perdebatan abadi atas peran eksperimen, dicontohkan dalam Schrödinger Cat eksperimen pikiran . This leads to the well-known uncertainty principle as well as the enduring debate over the role of the experimenter, epitomised in the Schrödinger's Cat thought experiment .
Mekanika kuantum berbeda secara signifikan dari mekanika klasik dalam prediksi ketika skala pengamatan menjadi sebanding dengan skala atom dan sub-atom, yang disebut kuantum alam . Quantum mechanics differs significantly from classical mechanics in its predictions when the scale of observations becomes comparable to the atomic and sub-atomic scale, the so-called quantum realm . Namun, banyak makroskopik sifat sistem hanya dapat sepenuhnya dipahami dan dijelaskan dengan menggunakan mekanika kuantum. However, many macroscopic properties of systems can only be fully understood and explained with the use of quantum mechanics. Fenomena seperti superkonduktivitas , sifat-sifat bahan seperti semikonduktor dan nuklir dan kimia mekanisme reaksi diamati sebagai perilaku makroskopik, tidak bisa dijelaskan menggunakan mekanika klasik. Phenomena such as superconductivity , the properties of materials such as semiconductors and nuclear and chemical reaction mechanisms observed as macroscopic behaviour, cannot be explained using classical mechanics.
Istilah ini diciptakan oleh Max Planck , dan berasal dari pengamatan bahwa beberapa kuantitas fisik dapat diubah hanya dengan jumlah diskrit atau kuanta , sebagai kelipatan dari konstanta Planck , bukannya mampu bervariasi secara kontinyu atau dengan jumlah yang sewenang-wenang. The term was coined by Max Planck , and derives from the observation that some physical quantities can be changed only by discrete amounts, or quanta , as multiples of the Planck constant , rather than being capable of varying continuously or by any arbitrary amount. Sebagai contoh, momentum sudut , atau lebih umumnya tindakan , ^[2] dari sebuah elektron terikat ke atom atau molekul yang terkuantisasi. For example, the angular momentum , or more generally the action , ^{[ 2 ]} of an electron bound into an atom or molecule is quantized. Meskipun elektron terikat tidak menunjukkan tingkat energi terkuantisasi, salah satu yang terikat dalam suatu orbital atom memiliki nilai terkuantisasi momentum sudut. Although an unbound electron does not exhibit quantized energy levels, one which is bound in an atomic orbital has quantized values of angular momentum. Dalam konteks mekanika kuantum, dualitas gelombang-partikel energi dan materi dan prinsip ketidakpastian memberikan pandangan terpadu dari perilaku foton , elektron dan atom-skala objek. In the context of quantum mechanics, the wave–particle duality of energy and matter and the uncertainty principle provide a unified view of the behavior of photons , electrons and other atomic-scale objects.
Para formulasi matematis mekanika kuantum yang abstrak. The mathematical formulations of quantum mechanics are abstract. Demikian pula, implikasi sering kontra-intuitif dalam hal fisika klasik . Similarly, the implications are often counter-intuitive in terms of classical physics . Inti dari formulasi matematis adalah fungsi gelombang (didefinisikan oleh persamaan gelombang Schrödinger ), yang menggambarkan amplitudo probabilitas posisi dan momentum partikel. The centerpiece of the mathematical formulation is the wavefunction (defined by Schrödinger's wave equation ), which describes the probability amplitude of the position and momentum of a particle. Manipulasi matematis dari fungsi gelombang biasanya melibatkan notasi bra-ket , yang membutuhkan pemahaman tentang bilangan kompleks dan functionals linear . Mathematical manipulations of the wavefunction usually involve the bra-ket notation , which requires an understanding of complex numbers and linear functionals . Fungsi gelombang memperlakukan objek sebagai osilator harmonik kuantum dan matematika mirip dengan yang dari resonansi akustik . The wavefunction treats the object as a quantum harmonic oscillator and the mathematics is akin to that of acoustic resonance .
Banyak hasil mekanika kuantum tidak memiliki model yang mudah divisualisasikan dalam hal mekanika klasik , misalnya, pada keadaan dasar dalam model kuantum mekanik adalah non-nol energi negara itu adalah energi negara diizinkan terendah dari suatu sistem, daripada sistem klasik tradisional yang dianggap sebagai sekadar beristirahat dengan nol energi kinetik. Many of the results of quantum mechanics do not have models that are easily visualized in terms of classical mechanics ; for instance, the ground state in the quantum mechanical model is a non-zero energy state that is the lowest permitted energy state of a system, rather than a traditional classical system that is thought of as simply being at rest with zero kinetic energy.
Pada dasarnya, ia mencoba untuk menjelaskan perilaku aneh dari materi dan energi pada tingkat sub-atomik upaya-an yang telah menghasilkan hasil yang lebih akurat dari fisika klasik dalam memprediksi bagaimana partikel individu berperilaku. Fundamentally, it attempts to explain the peculiar behaviour of matter and energy at the subatomic level—an attempt which has produced more accurate results than classical physics in predicting how individual particles behave. Tapi masih banyak anomali yang tidak dapat dijelaskan. But many unexplained anomalies remain.
Secara historis, versi awal mekanika kuantum dirumuskan dalam dekade pertama abad ke-20, sekitar waktu yang teori atom dan teori sel cahaya sebagaimana ditafsirkan oleh Einstein pertama kali datang ke secara luas diterima sebagai fakta ilmiah; teori-teori ini kemudian dapat dipandang sebagai teori kuantum dari materi dan radiasi elektromagnetik. Historically, the earliest versions of quantum mechanics were formulated in the first decade of the 20th Century, around the time that atomic theory and the corpuscular theory of light as interpreted by Einstein first came to be widely accepted as scientific fact; these later theories can be viewed as quantum theories of matter and electromagnetic radiation.
Setelah Schrödinger terobosan 's untuk menurunkan persamaan gelombang di pertengahan 1920-an, teori kuantum dirumuskan secara signifikan jauh dari teori kuantum lama , terhadap mekanika kuantum Werner Heisenberg , Max Born , Wolfgang Pauli dan rekan mereka, menjadi ilmu probabilitas berdasarkan interpretasi Kopenhagen dari Niels Bohr . Following Schrödinger 's breakthrough in deriving his wave equation in the mid-1920s, quantum theory was significantly reformulated away from the old quantum theory , towards the quantum mechanics of Werner Heisenberg , Max Born , Wolfgang Pauli and their associates, becoming a science of probabilities based upon the Copenhagen interpretation of Niels Bohr . Pada tahun 1930, teori telah dirumuskan lebih terpadu dan diresmikan oleh karya Paul Dirac dan John von Neumann , dengan penekanan lebih ditempatkan pada pengukuran , sifat statistik dari pengetahuan kita tentang realitas, dan spekulasi filosofis tentang peran pengamat . By 1930, the reformulated theory had been further unified and formalized by the work of Paul Dirac and John von Neumann , with a greater emphasis placed on measurement , the statistical nature of our knowledge of reality, and philosophical speculations about the role of the observer .
Interpretasi Kopenhagen dengan cepat menjadi (dan tetap) ^[3] interpretasi ortodoks. The Copenhagen interpretation quickly became (and remains) ^{[ 3 ]} the orthodox interpretation. Namun, karena tidak adanya bukti konklusif eksperimental juga terdapat berbagai interpretasi bersaing . However, due to the absence of conclusive experimental evidence there are also many competing interpretations .
Mekanika kuantum sejak bercabang ke dalam hampir setiap aspek fisika, dan masuk ke disiplin ilmu lain seperti kimia kuantum , kuantum elektronik , optik kuantum dan ilmu informasi kuantum . Quantum mechanics has since branched out into almost every aspect of physics, and into other disciplines such as quantum chemistry , quantum electronics , quantum optics and quantum information science . Fisika abad ke-19 Banyak telah kembali dievaluasi sebagai batas klasik mekanika kuantum dan perkembangan yang lebih maju dari segi teori medan kuantum , teori string , dan spekulatif gravitasi kuantum teori. Much 19th century physics has been re-evaluated as the classical limit of quantum mechanics and its more advanced developments in terms of quantum field theory , string theory , and speculative quantum gravity theories.

History

Artikel utama: Sejarah mekanika kuantum Main article: History of quantum mechanics

Sejarah mekanika kuantum tanggal kembali ke 1838 penemuan dari sinar katoda oleh Michael Faraday . The history of quantum mechanics dates back to the 1838 discovery of cathode rays by Michael Faraday . Hal ini diikuti oleh pernyataan 1859 dari radiasi benda hitam masalah oleh Gustav Kirchhoff , saran 1877 oleh Ludwig Boltzmann bahwa menyatakan energi dari sebuah sistem fisik dapat diskrit, dan tahun 1900 hipotesis kuantum Max Planck . ^[4] hipotesis Planck yang energi yang dipancarkan dan diserap dalam diskrit "kuanta", atau "unsur-unsur energi", justru cocok dengan pola yang diamati radiasi benda hitam. This was followed by the 1859 statement of the black body radiation problem by Gustav Kirchhoff , the 1877 suggestion by Ludwig Boltzmann that the energy states of a physical system can be discrete, and the 1900 quantum hypothesis of Max Planck . ^{[ 4 ]} Planck's hypothesis that energy is radiated and absorbed in discrete "quanta", or "energy elements", precisely matched the observed patterns of black body radiation. Menurut Planck, masing-masing elemen energi E sebanding dengan yang frekuensi ν: According to Planck, each energy element E is proportional to its frequency ν :

di mana h adalah konstanta Planck . where h is Planck's constant . Planck hati-hati menekankan bahwa ini hanyalah sebuah aspek dari proses penyerapan dan emisi radiasi dan tidak ada hubungannya dengan realitas fisik dari radiasi itu sendiri. ^[5] Namun, pada tahun 1905 Albert Einstein ditafsirkan Planck hipotesis kuantum realistis dan menggunakannya untuk menjelaskan efek fotolistrik , yang bersinar cahaya pada bahan-bahan tertentu dapat mengeluarkan elektron dari material. Planck cautiously insisted that this was simply an aspect of the processes of absorption and emission of radiation and had nothing to do with the physical reality of the radiation itself. ^{[ 5 ]} However, in 1905 Albert Einstein interpreted Planck's quantum hypothesis realistically and used it to explain the photoelectric effect , in which shining light on certain materials can eject electrons from the material.
Dasar-dasar mekanika kuantum didirikan selama paruh pertama abad kedua puluh oleh Niels Bohr, Werner Heisenberg, Max Planck, Louis de Broglie , Albert Einstein , Erwin Schrodinger , Max Born, John von Neumann, Paul Dirac, Wolfgang Pauli, David Hilbert , dan lain-lain . The foundations of quantum mechanics were established during the first half of the twentieth century by Niels Bohr, Werner Heisenberg, Max Planck, Louis de Broglie , Albert Einstein , Erwin Schrödinger , Max Born, John von Neumann, Paul Dirac, Wolfgang Pauli, David Hilbert , and others . Pada pertengahan 1920-an, perkembangan mekanika kuantum menjadi yang menyebabkan perumusan standar untuk fisika atom. In the mid-1920s, developments in quantum mechanics led to its becoming the standard formulation for atomic physics. Pada musim panas tahun 1925, Bohr dan Heisenberg yang diterbitkan hasil yang menutup "Teori Kuantum Lama" . In the summer of 1925, Bohr and Heisenberg published results that closed the "Old Quantum Theory" . Karena menghormati negara ganda mereka sebagai partikel, kuanta cahaya kemudian disebut foton (1926). Out of deference to their dual state as particles, light quanta came to be called photons (1926). Dari dalil yang sederhana Einstein lahir sebuah kebingungan berdebat, teori dan pengujian. From Einstein's simple postulation was born a flurry of debating, theorizing and testing. Dengan demikian seluruh bidang fisika kuantum muncul, yang mengarah ke penerimaan yang lebih luas pada Kelima Konferensi Solvay pada tahun 1927. Thus the entire field of quantum physics emerged, leading to its wider acceptance at the Fifth Solvay Conference in 1927.
Yang lainnya teladan yang menyebabkan mekanika kuantum adalah studi tentang gelombang elektromagnetik seperti cahaya. The other exemplar that led to quantum mechanics was the study of electromagnetic waves such as light. Ketika ditemukan pada tahun 1900 oleh Max Planck bahwa energi gelombang dapat digambarkan sebagai yang terdiri dari paket kecil atau kuanta, Albert Einstein lebih lanjut mengembangkan ide ini untuk menunjukkan bahwa gelombang elektromagnetik seperti cahaya dapat digambarkan sebagai sebuah partikel - kemudian disebut foton - dengan kuanta diskrit energi yang tergantung pada frekuensi. ^[6] Hal ini menyebabkan teori kesatuan antara partikel subatom dan gelombang elektromagnetik disebut Dualitas gelombang-partikel di mana partikel dan gelombang itu bukanlah satu atau yang lain, tapi tertentu sifat dari keduanya. When it was found in 1900 by Max Planck that the energy of waves could be described as consisting of small packets or quanta, Albert Einstein further developed this idea to show that an electromagnetic wave such as light could be described as a particle - later called the photon - with a discrete quanta of energy that was dependent on its frequency. ^{[ 6 ]} This led to a theory of unity between subatomic particles and electromagnetic waves called wave–particle duality in which particles and waves were neither one nor the other, but had certain properties of both.
Sementara mekanika kuantum tradisional menggambarkan dunia yang sangat kecil, juga diperlukan untuk menjelaskan baru-baru ini diselidiki tertentu makroskopik sistem seperti superkonduktor dan superfluids . While quantum mechanics traditionally described the world of the very small, it is also needed to explain certain recently investigated macroscopic systems such as superconductors and superfluids .
Kata kuantum berasal dari bahasa Latin , berarti "seberapa besar" atau "seberapa banyak". ^[7] Dalam mekanika kuantum, mengacu pada sebuah unit diskrit bahwa teori kuantum memberikan ke beberapa kuantitas fisik , seperti energi dari sebuah atom saat istirahat ( lihat Gambar 1). The word quantum derives from Latin , meaning "how great" or "how much". ^{[ 7 ]} In quantum mechanics, it refers to a discrete unit that quantum theory assigns to certain physical quantities , such as the energy of an atom at rest (see Figure 1). Penemuan bahwa partikel-partikel diskrit paket energi dengan gelombang-seperti properti menyebabkan cabang fisika yang berhubungan dengan sistem atom dan sub-atom yang hari ini disebut mekanika kuantum. The discovery that particles are discrete packets of energy with wave-like properties led to the branch of physics dealing with atomic and sub-atomic systems which is today called quantum mechanics. Ini adalah dasar matematika kerangka banyak bidang fisika dan kimia , termasuk fisika benda terkondensasi , fisika zat padat , fisika atom , fisika molekuler , fisika komputasi , kimia komputasi , kimia kuantum , fisika partikel , kimia nuklir , dan fisika nuklir . ^{[ 8]} Beberapa aspek fundamental dari teori masih aktif dipelajari. ^[9] It is the underlying mathematical framework of many fields of physics and chemistry , including condensed matter physics , solid-state physics , atomic physics , molecular physics , computational physics , computational chemistry , quantum chemistry , particle physics , nuclear chemistry , and nuclear physics . ^{[ 8 ]} Some fundamental aspects of the theory are still actively studied. ^{[ 9 ]}
Mekanika kuantum sangat penting untuk memahami perilaku sistem di atom skala panjang dan lebih kecil. Quantum mechanics is essential to understand the behavior of systems at atomic length scales and smaller. Sebagai contoh, jika mekanika klasik diatur kerja atom, elektron cepat akan perjalanan menuju dan berbenturan dengan inti , sehingga atom stabil mustahil. For example, if classical mechanics governed the workings of an atom, electrons would rapidly travel towards and collide with the nucleus , making stable atoms impossible. Namun, dalam alam elektron biasanya tetap dalam, pasti non-deterministik jalan "diolesi" (gelombang-partikel fungsi gelombang) orbital sekitar atau melalui inti, menantang elektromagnetisme klasik . ^[10] However, in the natural world the electrons normally remain in an uncertain, non-deterministic "smeared" (wave–particle wave function) orbital path around or through the nucleus, defying classical electromagnetism . ^{[ 10 ]}
Mekanika kuantum pada awalnya dikembangkan untuk memberikan penjelasan yang lebih baik dari atom, khususnya perbedaan dalam spektrum dari cahaya yang dipancarkan oleh berbagai isotop dari unsur yang sama. Quantum mechanics was initially developed to provide a better explanation of the atom, especially the differences in the spectra of light emitted by different isotopes of the same element. Teori kuantum atom dikembangkan sebagai penjelasan bagi elektron yang tersisa di orbit , yang tidak dapat dijelaskan oleh hukum Newton tentang gerak dan hukum Maxwell elektromagnetisme klasik. The quantum theory of the atom was developed as an explanation for the electron remaining in its orbit , which could not be explained by Newton's laws of motion and Maxwell's laws of classical electromagnetism.
Secara umum, mekanika kuantum menggabungkan empat kelas fenomena fisika klasik yang tidak dapat menjelaskan: Broadly speaking, quantum mechanics incorporates four classes of phenomena for which classical physics cannot account:

• Para kuantisasi dari sifat fisik tertentu The quantization of certain physical properties
• Dualitas gelombang-partikel Wave–particle duality
• Para prinsip ketidakpastian The uncertainty principle
• Belitan kuantum . Quantum entanglement .

 

Read More

Thomas Alva Edison Biography

Thomas Alva Edison was the most prolific inventor in American history. He amassed a record 1,093 patents covering key innovations and minor improvements in wide range of fields, including telecommunications, electric power, sound recording, motion pictures, primary and storage batteries, and mining and cement technology. As important, he broadened the notion of invention to encompass what we now call innovation-invention, research, development, and commercialization-and invented the industrial research laboratory. Edison's role as an innovator is evident not only in his two major laboratories at Menlo Park and West Orange in New Jersey but in more than 300 companies formed worldwide to manufacture and market his inventions, many of which carried the Edison name, including some 200 Edison illuminating companies.

Early Life

Edison was born in 1847 in the canal town of Milan, Ohio, the last of seven children. His mother, Nancy, had been a school teacher; his father, Samuel, was a Canadian political firebrand who was exiled from his country. The family moved to Port Huron, Michigan, when Thomas was seven. He attended school briefly but was principally educated at home by his mother and in his father's library.

In 1859 Edison began working on a local branch of the Grand Trunk Railroad, selling newspapers, magazines, and candy. At one point he printed a newspaper on the train, and he also conducted chemical experiments in a baggage-car laboratory. By 1862 he had learned enough telegraphy to be employed as an operator in a local office.
From 1863 to 1867 he traveled through the Midwest as an itinerant telegrapher. During these years he read widely, studied and experimented with telegraph technology, and generally acquainted himself with electrical science.

 Early Inventive Career

In 1868 Edison became an independent inventor in Boston. Moving to New York the next year, he undertook inventive work for major telegraph companies. With money from those contracts he established a series of manufacturing shops in Newark, New Jersey, where he also employed experimental machinists to assist in his inventive work.
Edison soon acquired a reputation as a first-rank inventor. His work included stock tickers, fire alarms, methods of sending simultaneous messages on one wire, and an electrochemical telegraph to send messages by automatic machinery. The crowning achievement of this period was the quadruplex telegraph, which sent two messages simultaneously in each direction on one wire.
The problems of interfering signals in multiple telegraphy and high speed in automatic transmission forced Edison to extend his study of electromagnetism and chemistry. As a result, he introduced electrical and chemical laboratories into his experimental machine shops.
Near the end of 1875, observations of strange sparks in telegraph instruments led Edison into a public scientific controversy over what he called "etheric force," which only later was understood to be radio waves.

Menlo Park

In 1876, Edison created a freestanding industrial research facility incorporating both a machine shop and laboratories. Here in Menlo Park, on the rail line between New York City and Philadelphia, he developed three of his greatest inventions.

Urged by Western Union to develop a telephone that could compete with Alexander Graham Bell's, Edison invented a transmitter in which a button of compressed carbon changed its resistance as it was vibrated by the sound of the user's voice, a new principle that was used in telephones for the next century.
While working on the telephone in the summer of 1877, Edison discovered a method of recording sound, and in the late fall he unveiled the phonograph. This astounding instrument brought him world fame as the "Wizard of Menlo Park" and the "inventor of the age."
Finally, beginning in the fall of 1878, Edison devoted thirty months to developing a complete system of incandescent electric lighting. During his lamp experiments, he noticed an electrical phenomenon that became known as the "Edison effect," the basis for vacuum-tube electronics.
He left Menlo Park in 1881 to establish factories and offices in New York and elsewhere. Over the next five years he manufactured, improved, and installed his electrical system around the world. 

West Orange Laboratory

 In 1887, Edison built an industrial research laboratory in West Orange, New Jersey, that remained unsurpassed until the twentieth century. For four years it was the primary research facility for the Edison lighting companies, and Edison spent most of his time on that work. In 1888 and 1889, he concentrated for several months on a new version of the phonograph that recorded on wax cylinders.

Edison worked with William Dickson from 1888 till 1893 on a motion picture camera. Although Edison had always had experimental assistants, this was the clearest instance of a co-invention for which Edison received sole credit.
In 1887 Edison also returned to experiments on the electromagnetic separation and concentration of low-grade iron and gold ores, work he had begun in 1879. During the 1890's he built a full-scale plant in northern New Jersey to process iron ore. This venture was Edison's most notable commercial failure.

Later Years

 After the mining failure, Edison adapted some of the machinery to process Portland cement. A roasting kiln he developed became an industry standard. Edison cement was used for buildings, dams, and even Yankee Stadium.

In the early years of the automobile industry there were hopes for an electric vehicle, and Edison spent the first decade of the twentieth century trying to develop a suitable storage battery. Although gas power won out, Edison's battery was used extensively in industry.
In World War I the federal government asked Edison to head the Naval Consulting Board, which examined inventions submitted for military use. Edison worked on several problems, including submarine detectors and gun location techniques.
By the time of his death in 1931, Edison had received 1,093 U.S. patents, a total still untouched by any other inventor. Even more important, he created a model for modern industrial research.

Read More

isaac newton biography

S I R   I S A A C   N E W T O N
Dr Robert A. Hatch - University of Florida

---

Newton, Sir Isaac (1642-1727), English natural philosopher, generally regarded as the most original and influential theorist in the history of science. In addition to his invention of the infinitesimal calculus and a new theory of light and color, Newton transformed the structure of physical science with his three laws of motion and the law of universal gravitation. As the keystone of the scientific revolution of the 17th century, Newton's work combined the contributions of Copernicus, Kepler, Galileo, Descartes, and others into a new and powerful synthesis. Three centuries later the resulting structure - classical mechanics - continues to be a useful but no less elegant monument to his genius. Life & Character - Isaac Newton was born prematurely on Christmas day 1642 (4 January 1643, New Style) in Woolsthorpe, a hamlet near Grantham in Lincolnshire. The posthumous son of an illiterate yeoman (also named Isaac), the fatherless infant was small enough at birth to fit 'into a quartpot.' When he was barely three years old Newton's mother, Hanna (Ayscough), placed her first born with his grandmother in order to remarry and raise a second family with Barnabas Smith, a wealthy rector from nearby North Witham. Much has been made of Newton's posthumous birth, his prolonged separation from his mother, and his unrivaled hatred of his stepfather. Until Hanna returned to Woolsthorpe in 1653 after the death of her second husband, Newton was denied his mother's attention, a possible clue to his complex character. Newton's childhood was anything but happy, and throughout his life he verged on emotional collapse, occasionally falling into violent and vindictive attacks against friend and foe alike.
With his mother's return to Woolsthorpe in 1653, Newton was taken from school to fulfill his birthright as a farmer. Happily, he failed in this calling, and returned to King's School at Grantham to prepare for entrance to Trinity College, Cambridge. Numerous anecdotes survive from this period about Newton's absent-mindedness as a fledging farmer and his lackluster performance as a student. But the turning point in Newton's life came in June 1661 when he left Woolsthorpe for Cambridge University. Here Newton entered a new world, one he could eventually call his own.
Although Cambridge was an outstanding center of learning, the spirit of the scientific revolution had yet to penetrate its ancient and somewhat ossified curriculum. Little is known of Newton's formal studies as an undergraduate, but he likely received large doses of Aristotle as well as other classical authors. And by all appearances his academic performance was undistinguished. In 1664 Isaac Barrow, Lucasian Professor of Mathematics at Cambridge, examined Newton's understanding of Euclid and found it sorely lacking. We now know that during his undergraduate years Newton was deeply engrossed in private study, that he privately mastered the works of René Descartes, Pierre Gassendi, Thomas Hobbes, and other major figures of the scientific revolution. A series of extant notebooks shows that by 1664 Newton had begun to master Descartes' Géométrie and other forms of mathematics far in advance of Euclid's Elements. Barrow, himself a gifted mathematician, had yet to appreciate Newton's genius.
In 1665 Newton took his bachelor's degree at Cambridge without honors or distinction. Since the university was closed for the next two years because of plague, Newton returned to Woolsthorpe in midyear. There, in the following 18 months, he made a series of original contributions to science. As he later recalled, 'All this was in the two plague years of 1665 and 1666, for in those days I was in my prime of age for invention, and minded mathematics and philosophy more than at any time since.' In mathematics Newton conceived his 'method of fluxions' (infinitesimal calculus), laid the foundations for his theory of light and color, and achieved significant insight into the problem of planetary motion, insights that eventually led to the publication of his Principia (1687).
In April 1667, Newton returned to Cambridge and, against stiff odds, was elected a minor fellow at Trinity. Success followed good fortune. In the next year he became a senior fellow upon taking his master of arts degree, and in 1669, before he had reached his 27th birthday, he succeeded Isaac Barrow as Lucasian Professor of Mathematics. The duties of this appointment offered Newton the opportunity to organize the results of his earlier optical researches, and in 1672, shortly after his election to the Royal Society, he communicated his first public paper, a brilliant but no less controversial study on the nature of color.
In the first of a series of bitter disputes, Newton locked horns with the society's celebrated curator of experiments, the bright but brittle Robert Hooke. The ensuing controversy, which continued until 1678, established a pattern in Newton's behavior. After an initial skirmish, he quietly retreated. Nonetheless, in 1675 Newton ventured another yet another paper, which again drew lightning, this time charged with claims that he had plagiarized from Hooke. The charges were entirely ungrounded. Twice burned, Newton withdrew.
In 1678, Newton suffered a serious emotional breakdown, and in the following year his mother died. Newton's response was to cut off contact with others and engross himself in alchemical research. These studies, once an embarrassment to Newton scholars, were not misguided musings but rigorous investigations into the hidden forces of nature. Newton's alchemical studies opened theoretical avenues not found in the mechanical philosophy, the world view that sustained his early work. While the mechanical philosophy reduced all phenomena to the impact of matter in motion, the alchemical tradition upheld the possibility of attraction and repulsion at the particulate level. Newton's later insights in celestial mechanics can be traced in part to his alchemical interests. By combining action-at-a-distance and mathematics, Newton transformed the mechanical philosophy by adding a mysterious but no less measurable quantity, gravitational force.
In 1666, as tradition has it, Newton observed the fall of an apple in his garden at Woolsthorpe, later recalling, 'In the same year I began to think of gravity extending to the orb of the Moon.' Newton's memory was not accurate. In fact, all evidence suggests that the concept of universal gravitation did not spring full-blown from Newton's head in 1666 but was nearly 20 years in gestation. Ironically, Robert Hooke helped give it life. In November 1679, Hooke initiated an exchange of letters that bore on the question of planetary motion. Although Newton hastily broke off the correspondence, Hooke's letters provided a conceptual link between central attraction and a force falling off with the square of distance. Sometime in early 1680, Newton appears to have quietly drawn his own conclusions.
Meanwhile, in the coffeehouses of London, Hooke, Edmund Halley, and Christopher Wren struggled unsuccessfully with the problem of planetary motion. Finally, in August 1684, Halley paid a legendary visit to Newton in Cambridge, hoping for an answer to his riddle:  What type of curve does a planet describe in its orbit around the sun, assuming an inverse square law of attraction? When Halley posed the question, Newton's ready response was 'an ellipse.' When asked how he knew it was an ellipse Newton replied that he had already calculated it. Although Newton had privately answered one of the riddles of the universe--and he alone possessed the mathematical ability to do so--he had characteristically misplaced the calculation. After further discussion he promised to send Halley a fresh calculation forthwith. In partial fulfillment of his promise Newton produced his De Motu of 1684. From that seed, after nearly two years of intense labor, the Philosophiae Naturalis Principia Mathematica appeared. Arguably, it is the most important book published in the history of science. But if the Principia was Newton's brainchild, Hooke and Halley were nothing less than midwives.
Although the Principia was well received, its future was cast in doubt before it appeared. Here again Hooke was center stage, this time claiming (not without justification) that his letters of 1679-1680 earned him a role in Newton's discovery. But to no effect. Newton was so furious with Hooke that he threatened to suppress Book III of the Principia altogether, finally denouncing science as 'an impertinently litigious lady.' Newton calmed down and finally consented to publication. But instead of acknowledging Hooke's contribution Newton systematically deleted every possible mention of Hooke's name. Newton's hatred for Hooke was consumptive. Indeed, Newton later withheld publication of his Opticks (1704) and virtually withdrew from the Royal Society until Hooke's death in 1703.
After publishing the Principia, Newton became more involved in public affairs. In 1689 he was elected to represent Cambridge in Parliament, and during his stay in London he became acquainted with John Locke, the famous philosopher, and Nicolas Fatio de Duillier, a brilliant young mathematician who became an intimate friend. In 1693, however, Newton suffered a severe nervous disorder, not unlike his breakdown of 1677-1678. The cause is open to interpretation: overwork; the stress of controversy; the unexplained loss of friendship with Fatio; or perhaps chronic mercury poisoning, the result of nearly three decades of alchemical research. Each factor may have played a role. We only know Locke and Samuel Pepys received strange and seemingly deranged letters that prompted concern for Newton's 'discomposure in head, or mind, or both.' Whatever the cause, shortly after his recovery Newton sought a new position in London. In 1696, with the help of Charles Montague, a fellow of Trinity and later earl of Halifax, Newton was appointed Warden and then Master of the Mint. His new position proved 'most proper,' and he left Cambridge for London without regret.
During his London years Newton enjoyed power and worldly success. His position at the Mint assured a comfortable social and economic status, and he was an active and able administrator. After the death of Hooke in 1703, Newton was elected president of the Royal Society and was annually reelected until his death. In 1704 he published his second major work, the Opticks, based largely on work completed decades before. He was knighted in 1705.
Although his creative years had passed, Newton continued to exercise a profound influence on the development of science. In effect, the Royal Society was Newton's instrument, and he played it to his personal advantage. His tenure as president has been described as tyrannical and autocratic, and his control over the lives and careers of younger disciples was all but absolute. Newton could not abide contradiction or controversy - his quarrels with Hooke provide singular examples. But in later disputes, as president of the Royal Society, Newton marshaled all the forces at his command. For example, he published Flamsteed's astronomical observations - the labor of a lifetime - without the author's permission; and in his priority dispute with Leibniz concerning the calculus, Newton enlisted younger men to fight his war of words, while behind the lines he secretly directed charge and countercharge. In the end, the actions of the Society were little more than extensions of Newton's will, and until his death he dominated the landscape of science without rival. He died in London on March 20, 1727 (March 31, New Style).
 

Scientific Achievements Mathematics - The origin of Newton's interest in mathematics can be traced to his undergraduate days at Cambridge. Here Newton became acquainted with a number of contemporary works, including an edition of Descartes Géométrie, John Wallis' Arithmetica infinitorum, and other works by prominent mathematicians. But between 1664 and his return to Cambridge after the plague, Newton made fundamental contributions to analytic geometry, algebra, and calculus. Specifically, he discovered the binomial theorem, new methods for expansion of infinite series, and his 'direct and inverse method of fluxions.' As the term implies, fluxional calculus is a method for treating changing or flowing quantities. Hence, a 'fluxion' represents the rate of change of a 'fluent'--a continuously changing or flowing quantity, such as distance, area, or length. In essence, fluxions were the first words in a new language of physics.
Newton's creative years in mathematics extended from 1664 to roughly the spring of 1696. Although his predecessors had anticipated various elements of the calculus, Newton generalized and integrated these insights while developing new and more rigorous methods. The essential elements of his thought were presented in three tracts, the first appearing in a privately circulated treatise, De analysi (On Analysis),which went unpublished until 1711. In 1671, Newton developed a more complete account of his method of infinitesimals, which appeared nine years after his death as Methodus fluxionum et serierum infinitarum (The Method of Fluxions and Infinite Series, 1736). In addition to these works, Newton wrote four smaller tracts, two of which were appended to his Opticks of 1704.
Newton and Leibniz. Next to its brilliance, the most characteristic feature of Newton's mathematical career was delayed publication. Newton's priority dispute with Leibniz is a celebrated but unhappy example. Gottfried Wilhelm Leibniz, Newton's most capable adversary, began publishing papers on calculus in 1684, almost 20 years after Newton's discoveries commenced. The result of this temporal discrepancy was a bitter dispute that raged for nearly two decades. The ordeal began with rumors that Leibniz had borrowed ideas from Newton and rushed them into print. It ended with charges of dishonesty and outright plagiarism. The Newton-Leibniz priority dispute--which eventually extended into philosophical areas concerning the nature of God and the universe--ultimately turned on the ambiguity of priority. It is now generally agreed that Newton and Leibniz each developed the calculus independently, and hence they are considered co-discoverers. But while Newton was the first to conceive and develop his method of fluxions, Leibniz was the first to publish his independent results.
Optics. Newton's optical research, like his mathematical investigations, began during his undergraduate years at Cambridge. But unlike his mathematical work, Newton's studies in optics quickly became public. Shortly after his election to the Royal Society in 1671, Newton published his first paper in the Philosophical Transactions of the Royal Society. This paper, and others that followed, drew on his undergraduate researches as well as his Lucasian lectures at Cambridge.
In 1665-1666, Newton performed a number of experiments on the composition of light. Guided initially by the writings of Kepler and Descartes, Newton's main discovery was that visible (white) light is heterogeneous--that is, white light is composed of colors that can be considered primary. Through a brilliant series of experiments, Newton demonstrated that prisms separate rather than modify white light. Contrary to the theories of Aristotle and other ancients, Newton held that white light is secondary and heterogeneous, while the separate colors are primary and homogeneous. Of perhaps equal importance, Newton also demonstrated that the colors of the spectrum, once thought to be qualities, correspond to an observed and quantifiable 'degree of Refrangibility.'
The Crucial Experiment. Newton's most famous experiment, the experimentum crucis, demonstrated his theory of the composition of light. Briefly, in a dark room Newton allowed a narrow beam of sunlight to pass from a small hole in a window shutter through a prism, thus breaking the white light into an oblong spectrum on a board. Then, through a small aperture in the board, Newton selected a given color (for example, red) to pass through yet another aperture to a second prism, through which it was refracted onto a second board. What began as ordinary white light was thus dispersed through two prisms.
Newton's 'crucial experiment' demonstrated that a selected color leaving the first prism could not be separated further by the second prism. The selected beam remained the same color, and its angle of refraction was constant throughout. Newton concluded that white light is a 'Heterogeneous mixture of differently refrangible Rays' and that colors of the spectrum cannot themselves be individually modified, but are 'Original and connate properties.'
Newton probably conducted a number of his prism experiments at Cambridge before the plague forced him to return to Woolsthorpe. His Lucasian lectures, later published in part as Optical Lectures (1728), supplement other researches published in the Society's Transactions dating from February 1672.
The Opticks. The Opticks of 1704, which first appeared in English, is Newton's most comprehensive and readily accessible work on light and color. In Newton's words, the purpose of the Opticks was 'not to explain the Properties of Light by Hypotheses, but to propose and prove them by Reason and Experiments.' Divided into three books, the Opticks moves from definitions, axioms, propositions, and theorems to proof by experiment. A subtle blend of mathematical reasoning and careful observation, the Opticks became the model for experimental physics in the 18th century.
The Corpuscular Theory. But the Opticks contained more than experimental results. During the 17th century it was widely held that light, like sound, consisted of a wave or undulatory motion, and Newton's major critics in the field of optics--Robert Hooke and Christiaan Huygens--were articulate spokesmen for this theory. But Newton disagreed. Although his views evolved over time, Newton's theory of light was essentially corpuscular, or particulate. In effect, since light (unlike sound) travels in straight lines and casts a sharp shadow, Newton suggested that light was composed of discrete particles moving in straight lines in the manner of inertial bodies. Further, since experiment had shown that the properties of the separate colors of light were constant and unchanging, so too, Newton reasoned, was the stuff of light itself-- particles.
At various points in his career Newton in effect combined the particle and wave theories of light. In his earliest dispute with Hooke and again in his Opticks of 1717, Newton considered the possibility of an ethereal substance--an all-pervasive elastic material more subtle than air--that would provide a medium for the propagation of waves or vibrations. From the outset Newton rejected the basic wave models of Hooke and Huygens, perhaps because they overlooked the subtlety of periodicity.
The question of periodicity arose with the phenomenon known as 'Newton's rings.' In book II of the Opticks, Newton describes a series of experiments concerning the colors of thin films. His most remarkable observation was that light passing through a convex lens pressed against a flat glass plate produces concentric colored rings (Newton's rings) with alternating dark rings. Newton attempted to explain this phenomenon by employing the particle theory in conjunction with his hypothesis of 'fits of easy transmission [refraction] and reflection.' After making careful measurements, Newton found that the thickness of the film of air between the lens (of a given curvature) and the glass corresponded to the spacing of the rings. If dark rings occurred at thicknesses of 0, 2, 4, 6... , then the colored rings corresponded to an odd number progression, 1, 3, 5, 7, .... Although Newton did not speculate on the cause of this periodicity, his initial association of 'Newton's rings' with vibrations in a medium suggests his willingness to modify but not abandon the particle theory.
The Opticks was Newton's most widely read work. Following the first edition, Latin versions appeared in 1706 and 1719, and second and third English editions in 1717 and 1721. Perhaps the most provocative part of the Opticks is the section known as the 'Queries,' which Newton placed at the end of the book. Here he posed questions and ventured opinions on the nature of light, matter, and the forces of nature.
Mechanics. Newton's research in dynamics falls into three major periods: the plague years 1664-1666, the investigations of 1679-1680, following Hooke's correspondence, and the period 1684-1687, following Halley's visit to Cambridge. The gradual evolution of Newton's thought over these two decades illustrates the complexity of his achievement as well as the prolonged character of scientific 'discovery.'
While the myth of Newton and the apple maybe true, the traditional account of Newton and gravity is not. To be sure, Newton's early thoughts on gravity began in Woolsthorpe, but at the time of his famous 'moon test' Newton had yet to arrive at the concept of gravitational attraction. Early manuscripts suggest that in the mid-1660's, Newton did not think in terms of the moon's central attraction toward the earth but rather of the moon's centrifugal tendency to recede. Under the influence of the mechanical philosophy, Newton had yet to consider the possibility of action- at-a-distance; nor was he aware of Kepler's first two planetary hypotheses. For historical, philosophical, and mathematical reasons, Newton assumed the moon's centrifugal 'endeavour' to be equal and opposite to some unknown mechanical constraint. For the same reasons, he also assumed a circular orbit and an inverse square relation. The latter was derived from Kepler's third hypothesis (the square of a planet's orbital period is proportional to the cube of its mean distance from the sun), the formula for centrifugal force (the centrifugal force on a revolving body is proportional to the square of its velocity and inversely proportional to the radius of its orbit), and the assumption of circular orbits.
The next step was to test the inverse square relation against empirical data. To do this Newton, in effect, compared the restraint on the moon's 'endeavour' to recede with the observed rate of acceleration of falling objects on earth. The problem was to obtain accurate data. Assuming Galileo's estimate that the moon is 60 earth radii from the earth, the restraint on the moon should have been 1/3600 (1/60²) of the gravitational acceleration on earth. But Newton's estimate of the size of the earth was too low, and his calculation showed the effect on the moon to be about 1/4000 of that on earth. As Newton later described it, the moon test answered 'pretty nearly.' But the figures for the moon were not exact, and Newton abandoned the problem.
In late 1679 and early 1680 an exchange of letters with Hooke renewed Newton's interest. In November 1679, nearly 15 years after the moon test, Hooke wrote Newton concerning a hypothesis presented in his Attempt to Prove the Motion of the Earth (1674). Here Hooke proposed that planetary orbits result from a tangential motion and 'an attractive motion towards the centrall body.' In later letters Hooke further specified a central attracting force that fell off with the square of distance. As a result of this exchange Newton rejected his earlier notion of centrifugal tendencies in favor of central attraction. Hooke's letters provided crucial insight. But in retrospect, if Hooke's intuitive power seems unparalleled, it never approached Newton's mathematical power in principle or in practice.
When Halley visited Cambridge in 1684, Newton had already demonstrated the relation between an inverse square attraction and elliptical orbits. To Halley's 'joy and amazement,' Newton apparently succeeded where he and others failed. With this, Halley's role shifted, and he proceeded to guide Newton toward publication. Halley personally financed the Principia and saw it through the press to publication in July 1687.
The Principia. Newton's masterpiece is divided into three books. Book I of the Principia begins with eight definitions and three axioms, the latter now known as Newton's laws of motion. No discussion of Newton would be complete without them: (1) Every body continues in its state of rest, or uniform motion in a straight line, unless it is compelled to change that state by forces impressed on it (inertia). (2) The change in motion is proportional to the motive force impressed and is made in the direction of the straight line in which that force is impressed (F = ma). (3) To every action there is always an opposed and equal reaction. Following these axioms, Newton proceeds step by step with propositions, theorems, and problems.
In Book II of the Principia, Newton treats the Motion of bodies through resisting mediums as well as the motion of fluids themselves. Since Book II was not part of Newton's initial outline, it has traditionally seemed somewhat out of place. Nonetheless, it is noteworthy that near the end of Book II (Section IX) Newton demonstrates that the vortices invoked by Descartes to explain planetary motion could not be self-sustaining; nor was the vortex theory consistent with Kepler's three planetary rules. The purpose of Book II then becomes clear. After discrediting Descartes' system, Newton concludes: 'How these motions are performed in free space without vortices, may be understood by the first book; and I shall now more fully treat of it in the following book.'
In Book III, subtitled the System of the World, Newton extended his three laws of motion to the frame of the world, finally demonstrating 'that there is a power of gravity tending to all bodies, proportional to the several quantities of matter which they contain.' Newton's law of universal gravitation states that F = G Mm/R²; that is, that all matter is mutually attracted with a force (F) proportional to the product of their masses (Mm) and inversely proportional to the square of distance (R2) between them. G is a constant whose value depends on the units used for mass and distance. To demonstrate the power of his theory, Newton used gravitational attraction to explain the motion of the planets and their moons, the precession of equinoxes, the action of the tides, and the motion of comets. In sum, Newton's universe united heaven and earth with a single set of laws. It became the physical and intellectual foundation of the modern world view.
Perhaps the most powerful and influential scientific treatise ever published, the Principia appeared in two further editions during Newton's lifetime, in 1713 and 1726.
Other Researches. Throughout his career Newton conducted research in theology and history with the same passion that he pursued alchemy and science. Although some historians have neglected Newton's nonscientific writings, there is little doubt of his devotion to these subjects, as his manuscripts amply attest. Newton's writings on theological and biblical subjects alone amount to about 1.3 million words, the equivalent of 20 of today's standard length books. Although these writings say little about Newtonian science, they tell us a good deal about Isaac Newton.
Newton's final gesture before death was to refuse the sacrament, a decision of some consequence in the 18th century. Although Newton was dutifully raised in the Protestant tradition his mature views on theology were neither Protestant, traditional, nor orthodox. In the privacy of his thoughts and writings, Newton rejected a host of doctrines he considered mystical, irrational, or superstitious. In a word, he was a Unitarian.
Newton's research outside of science--in theology, prophecy, and history--was a quest for coherence and unity. His passion was to unite knowledge and belief, to reconcile the Book of Nature with the Book of Scripture. But for all the elegance of his thought and the boldness of his quest, the riddle of Isaac Newton remained. In the end, Newton is as much an enigma to us as he was, no doubt, to himself.
 
Robert A. Hatch
University of Florida

Read More

Archimedes biography

Archimedes' father was Phidias, an astronomer. We know nothing else about Phidias other than this one fact and we only know this since Archimedes gives us this information in one of his works, The Sandreckoner. A friend of Archimedes called Heracleides wrote a biography of him but sadly this work is lost. How our knowledge of Archimedes would be transformed if this lost work were ever found, or even extracts found in the writing of others.

Archimedes was a native of Syracuse, Sicily. It is reported by some authors that he visited Egypt and there invented a device now known as Archimedes' screw. This is a pump, still used in many parts of the world. It is highly likely that, when he was a young man, Archimedes studied with the successors of Euclid in Alexandria. Certainly he was completely familiar with the mathematics developed there, but what makes this conjecture much more certain, he knew personally the mathematicians working there and he sent his results to Alexandria with personal messages. He regarded Conon of Samos, one of the mathematicians at Alexandria, both very highly for his abilities as a mathematician and he also regarded him as a close friend.

In the preface to On spirals Archimedes relates an amusing story regarding his friends in Alexandria. He tells us that he was in the habit of sending them statements of his latest theorems, but without giving proofs. Apparently some of the mathematicians there had claimed the results as their own so Archimedes says that on the last occasion when he sent them theorems he included two which were false [3]:-

... so that those who claim to discover everything, but produce no proofs of the same, may be confuted as having pretended to discover the impossible.

Other than in the prefaces to his works, information about Archimedes comes to us from a number of sources such as in stories from Plutarch, Livy, and others. Plutarch tells us that Archimedes was related to King Hieron II of Syracuse (see for example [3]):-

Archimedes ... in writing to King Hiero, whose friend and near relation he was....

Again evidence of at least his friendship with the family of King Hieron II comes from the fact that The Sandreckoner was dedicated to Gelon, the son of King Hieron.

There are, in fact, quite a number of references to Archimedes in the writings of the time for he had gained a reputation in his own time which few other mathematicians of this period achieved. The reason for this was not a widespread interest in new mathematical ideas but rather that Archimedes had invented many machines which were used as engines of war. These were particularly effective in the defence of Syracuse when it was attacked by the Romans under the command of Marcellus.

Plutarch writes in his work on Marcellus, the Roman commander, about how Archimedes' engines of war were used against the Romans in the siege of 212 BC:-

... when Archimedes began to ply his engines, he at once shot against the land forces all sorts of missile weapons, and immense masses of stone that came down with incredible noise and violence; against which no man could stand; for they knocked down those upon whom they fell in heaps, breaking all their ranks and files. In the meantime huge poles thrust out from the walls over the ships and sunk some by great weights which they let down from on high upon them; others they lifted up into the air by an iron hand or beak like a crane's beak and, when they had drawn them up by the prow, and set them on end upon the poop, they plunged them to the bottom of the sea; or else the ships, drawn by engines within, and whirled about, were dashed against steep rocks that stood jutting out under the walls, with great destruction of the soldiers that were aboard them. A ship was frequently lifted up to a great height in the air (a dreadful thing to behold), and was rolled to and fro, and kept swinging, until the mariners were all thrown out, when at length it was dashed against the rocks, or let fall.

Archimedes had been persuaded by his friend and relation King Hieron to build such machines:-

These machines [Archimedes] had designed and contrived, not as matters of any importance, but as mere amusements in geometry; in compliance with King Hiero's desire and request, some little time before, that he should reduce to practice some part of his admirable speculation in science, and by accommodating the theoretic truth to sensation and ordinary use, bring it more within the appreciation of the people in general.

Perhaps it is sad that engines of war were appreciated by the people of this time in a way that theoretical mathematics was not, but one would have to remark that the world is not a very different place at the end of the second millenium AD. Other inventions of Archimedes such as the compound pulley also brought him great fame among his contemporaries. Again we quote Plutarch:-

[Archimedes] had stated [in a letter to King Hieron] that given the force, any given weight might be moved, and even boasted, we are told, relying on the strength of demonstration, that if there were another earth, by going into it he could remove this. Hiero being struck with amazement at this, and entreating him to make good this problem by actual experiment, and show some great weight moved by a small engine, he fixed accordingly upon a ship of burden out of the king's arsenal, which could not be drawn out of the dock without great labour and many men; and, loading her with many passengers and a full freight, sitting himself the while far off, with no great endeavour, but only holding the head of the pulley in his hand and drawing the cords by degrees, he drew the ship in a straight line, as smoothly and evenly as if she had been in the sea.

Yet Archimedes, although he achieved fame by his mechanical inventions, believed that pure mathematics was the only worthy pursuit. Again Plutarch describes beautifully Archimedes attitude, yet we shall see later that Archimedes did in fact use some very practical methods to discover results from pure geometry:-

Archimedes possessed so high a spirit, so profound a soul, and such treasures of scientific knowledge, that though these inventions had now obtained him the renown of more than human sagacity, he yet would not deign to leave behind him any commentary or writing on such subjects; but, repudiating as sordid and ignoble the whole trade of engineering, and every sort of art that lends itself to mere use and profit, he placed his whole affection and ambition in those purer speculations where there can be no reference to the vulgar needs of life; studies, the superiority of which to all others is unquestioned, and in which the only doubt can be whether the beauty and grandeur of the subjects examined, of the precision and cogency of the methods and means of proof, most deserve our admiration.

His fascination with geometry is beautifully described by Plutarch:-

Oftimes Archimedes' servants got him against his will to the baths, to wash and anoint him, and yet being there, he would ever be drawing out of the geometrical figures, even in the very embers of the chimney. And while they were anointing of him with oils and sweet savours, with his fingers he drew lines upon his naked body, so far was he taken from himself, and brought into ecstasy or trance, with the delight he had in the study of geometry.

The achievements of Archimedes are quite outstanding. He is considered by most historians of mathematics as one of the greatest mathematicians of all time. He perfected a method of integration which allowed him to find areas, volumes and surface areas of many bodies. Chasles said that Archimedes' work on integration (see [7]):-

... gave birth to the calculus of the infinite conceived and brought to perfection by Kepler, Cavalieri, Fermat, Leibniz and Newton.

Archimedes was able to apply the method of exhaustion, which is the early form of integration, to obtain a whole range of important results and we mention some of these in the descriptions of his works below. Archimedes also gave an accurate approximation to π and showed that he could approximate square roots accurately. He invented a system for expressing large numbers. In mechanics Archimedes discovered fundamental theorems concerning the centre of gravity of plane figures and solids. His most famous theorem gives the weight of a body immersed in a liquid, called Archimedes' principle.

The works of Archimedes which have survived are as follows. On plane equilibriums (two books), Quadrature of the parabola, On the sphere and cylinder (two books), On spirals, On conoids and spheroids, On floating bodies (two books), Measurement of a circle, and The Sandreckoner. In the summer of 1906, J L Heiberg, professor of classical philology at the University of Copenhagen, discovered a 10^th century manuscript which included Archimedes' work The method. This provides a remarkable insight into how Archimedes discovered many of his results and we will discuss this below once we have given further details of what is in the surviving books.

The order in which Archimedes wrote his works is not known for certain. We have used the chronological order suggested by Heath in [7] in listing these works above, except for The Method which Heath has placed immediately before On the sphere and cylinder. The paper [47] looks at arguments for a different chronological order of Archimedes' works.

The treatise On plane equilibriums sets out the fundamental principles of mechanics, using the methods of geometry. Archimedes discovered fundamental theorems concerning the centre of gravity of plane figures and these are given in this work. In particular he finds, in book 1, the centre of gravity of a parallelogram, a triangle, and a trapezium. Book two is devoted entirely to finding the centre of gravity of a segment of a parabola. In the Quadrature of the parabola Archimedes finds the area of a segment of a parabola cut off by any chord.

In the first book of On the sphere and cylinder Archimedes shows that the surface of a sphere is four times that of a great circle, he finds the area of any segment of a sphere, he shows that the volume of a sphere is two-thirds the volume of a circumscribed cylinder, and that the surface of a sphere is two-thirds the surface of a circumscribed cylinder including its bases. A good discussion of how Archimedes may have been led to some of these results using infinitesimals is given in [14]. In the second book of this work Archimedes' most important result is to show how to cut a given sphere by a plane so that the ratio of the volumes of the two segments has a prescribed ratio.

In On spirals Archimedes defines a spiral, he gives fundamental properties connecting the length of the radius vector with the angles through which it has revolved. He gives results on tangents to the spiral as well as finding the area of portions of the spiral. In the work On conoids and spheroids Archimedes examines paraboloids of revolution, hyperboloids of revolution, and spheroids obtained by rotating an ellipse either about its major axis or about its minor axis. The main purpose of the work is to investigate the volume of segments of these three-dimensional figures. Some claim there is a lack of rigour in certain of the results of this work but the interesting discussion in [43] attributes this to a modern day reconstruction.

On floating bodies is a work in which Archimedes lays down the basic principles of hydrostatics. His most famous theorem which gives the weight of a body immersed in a liquid, called Archimedes' principle, is contained in this work. He also studied the stability of various floating bodies of different shapes and different specific gravities. In Measurement of the Circle Archimedes shows that the exact value of π lies between the values 3¹⁰/₇₁ and 3¹/₇. This he obtained by circumscribing and inscribing a circle with regular polygons having 96 sides.

The Sandreckoner is a remarkable work in which Archimedes proposes a number system capable of expressing numbers up to 8 × 10⁶³ in modern notation. He argues in this work that this number is large enough to count the number of grains of sand which could be fitted into the universe. There are also important historical remarks in this work, for Archimedes has to give the dimensions of the universe to be able to count the number of grains of sand which it could contain. He states that Aristarchus has proposed a system with the sun at the centre and the planets, including the Earth, revolving round it. In quoting results on the dimensions he states results due to Eudoxus, Phidias (his father), and to Aristarchus. There are other sources which mention Archimedes' work on distances to the heavenly bodies. For example in [59] Osborne reconstructs and discusses:-

...a theory of the distances of the heavenly bodies ascribed to Archimedes, but the corrupt state of the numerals in the sole surviving manuscript [due to Hippolytus of Rome, about 220 AD] means that the material is difficult to handle.

In the Method, Archimedes described the way in which he discovered many of his geometrical results (see [7]):-

... certain things first became clear to me by a mechanical method, although they had to be proved by geometry afterwards because their investigation by the said method did not furnish an actual proof. But it is of course easier, when we have previously acquired, by the method, some knowledge of the questions, to supply the proof than it is to find it without any previous knowledge.

Perhaps the brilliance of Archimedes' geometrical results is best summed up by Plutarch, who writes:-

It is not possible to find in all geometry more difficult and intricate questions, or more simple and lucid explanations. Some ascribe this to his natural genius; while others think that incredible effort and toil produced these, to all appearances, easy and unlaboured results. No amount of investigation of yours would succeed in attaining the proof, and yet, once seen, you immediately believe you would have discovered it; by so smooth and so rapid a path he leads you to the conclusion required.

Heath adds his opinion of the quality of Archimedes' work [7]:-

The treatises are, without exception, monuments of mathematical exposition; the gradual revelation of the plan of attack, the masterly ordering of the propositions, the stern elimination of everything not immediately relevant to the purpose, the finish of the whole, are so impressive in their perfection as to create a feeling akin to awe in the mind of the reader.

There are references to other works of Archimedes which are now lost. Pappus refers to a work by Archimedes on semi-regular polyhedra, Archimedes himself refers to a work on the number system which he proposed in the Sandreckoner, Pappus mentions a treatise On balances and levers, and Theon mentions a treatise by Archimedes about mirrors. Evidence for further lost works are discussed in [67] but the evidence is not totally convincing.

Archimedes was killed in 212 BC during the capture of Syracuse by the Romans in the Second Punic War after all his efforts to keep the Romans at bay with his machines of war had failed. Plutarch recounts three versions of the story of his killing which had come down to him. The first version:-

Archimedes ... was ..., as fate would have it, intent upon working out some problem by a diagram, and having fixed his mind alike and his eyes upon the subject of his speculation, he never noticed the incursion of the Romans, nor that the city was taken. In this transport of study and contemplation, a soldier, unexpectedly coming up to him, commanded him to follow to Marcellus; which he declining to do before he had worked out his problem to a demonstration, the soldier, enraged, drew his sword and ran him through.

The second version:-

... a Roman soldier, running upon him with a drawn sword, offered to kill him; and that Archimedes, looking back, earnestly besought him to hold his hand a little while, that he might not leave what he was then at work upon inconclusive and imperfect; but the soldier, nothing moved by his entreaty, instantly killed him.

Finally, the third version that Plutarch had heard:-

... as Archimedes was carrying to Marcellus mathematical instruments, dials, spheres, and angles, by which the magnitude of the sun might be measured to the sight, some soldiers seeing him, and thinking that he carried gold in a vessel, slew him.

Archimedes considered his most significant accomplishments were those concerning a cylinder circumscribing a sphere, and he asked for a representation of this together with his result on the ratio of the two, to be inscribed on his tomb. Cicero was in Sicily in 75 BC and he writes how he searched for Archimedes tomb (see for example [1]):-

... and found it enclosed all around and covered with brambles and thickets; for I remembered certain doggerel lines inscribed, as I had heard, upon his tomb, which stated that a sphere along with a cylinder had been put on top of his grave. Accordingly, after taking a good look all around ..., I noticed a small column arising a little above the bushes, on which there was a figure of a sphere and a cylinder... . Slaves were sent in with sickles ... and when a passage to the place was opened we approached the pedestal in front of us; the epigram was traceable with about half of the lines legible, as the latter portion was worn away.

It is perhaps surprising that the mathematical works of Archimedes were relatively little known immediately after his death. As Clagett writes in [1]:-

Unlike the Elements of Euclid, the works of Archimedes were not widely known in antiquity. ... It is true that ... individual works of Archimedes were obviously studied at Alexandria, since Archimedes was often quoted by three eminent mathematicians of Alexandria: Heron, Pappus and Theon.

Only after Eutocius brought out editions of some of Archimedes works, with commentaries, in the sixth century AD were the remarkable treatises to become more widely known. Finally, it is worth remarking that the test used today to determine how close to the original text the various versions of his treatises of Archimedes are, is to determine whether they have retained Archimedes' Dorian dialect.

Article by: J J O'Connor and E F Robertson

Read More

galileo biography

Galileo Galilei's parents were Vincenzo Galilei and Guilia Ammannati. Vincenzo, who was born in Florence in 1520, was a teacher of music and a fine lute player. After studying music in Venice he carried out experiments on strings to support his musical theories. Guilia, who was born in Pescia, married Vincenzo in 1563 and they made their home in the countryside near Pisa. Galileo was their first child and spent his early years with his family in Pisa.

In 1572, when Galileo was eight years old, his family returned to Florence, his father's home town. However, Galileo remained in Pisa and lived for two years with Muzio Tedaldi who was related to Galileo's mother by marriage. When he reached the age of ten, Galileo left Pisa to join his family in Florence and there he was tutored by Jacopo Borghini. Once he was old enough to be educated in a monastery, his parents sent him to the Camaldolese Monastery at Vallombrosa which is situated on a magnificent forested hillside 33 km southeast of Florence. The Camaldolese Order was independent of the Benedictine Order, splitting from it in about 1012. The Order combined the solitary life of the hermit with the strict life of the monk and soon the young Galileo found this life an attractive one. He became a novice, intending to join the Order, but this did not please his father who had already decided that his eldest son should become a medical doctor.

Vincenzo had Galileo return from Vallombrosa to Florence and give up the idea of joining the Camaldolese order. He did continue his schooling in Florence, however, in a school run by the Camaldolese monks. In 1581 Vincenzo sent Galileo back to Pisa to live again with Muzio Tedaldi and now to enrol for a medical degree at the University of Pisa. Although the idea of a medical career never seems to have appealed to Galileo, his father's wish was a fairly natural one since there had been a distinguished physician in his family in the previous century. Galileo never seems to have taken medical studies seriously, attending courses on his real interests which were in mathematics and natural philosophy. His mathematics teacher at Pisa was Filippo Fantoni, who held the chair of mathematics. Galileo returned to Florence for the summer vacations and there continued to study mathematics.

In the year 1582-83 Ostilio Ricci, who was the mathematician of the Tuscan Court and a former pupil of Tartaglia, taught a course on Euclid's Elements at the University of Pisa which Galileo attended. During the summer of 1583 Galileo was back in Florence with his family and Vincenzo encouraged him to read Galen to further his medical studies. However Galileo, still reluctant to study medicine, invited Ricci (also in Florence where the Tuscan court spent the summer and autumn) to his home to meet his father. Ricci tried to persuade Vincenzo to allow his son to study mathematics since this was where his interests lay. Certainly Vincenzo did not like the idea and resisted strongly but eventually he gave way a little and Galileo was able to study the works of Euclid and Archimedes from the Italian translations which Tartaglia had made. Of course he was still officially enrolled as a medical student at Pisa but eventually, by 1585, he gave up this course and left without completing his degree.

Galileo began teaching mathematics, first privately in Florence and then during 1585-86 at Siena where he held a public appointment. During the summer of 1586 he taught at Vallombrosa, and in this year he wrote his first scientific book The little balance [La Balancitta] which described Archimedes' method of finding the specific gravities (that is the relative densities) of substances using a balance. In the following year he travelled to Rome to visit Clavius who was professor of mathematics at the Jesuit Collegio Romano there. A topic which was very popular with the Jesuit mathematicians at this time was centres of gravity and Galileo brought with him some results which he had discovered on this topic. Despite making a very favourable impression on Clavius, Galileo failed to gain an appointment to teach mathematics at the University of Bologna.

After leaving Rome Galileo remained in contact with Clavius by correspondence and Guidobaldo del Monte was also a regular correspondent. Certainly the theorems which Galileo had proved on the centres of gravity of solids, and left in Rome, were discussed in this correspondence. It is also likely that Galileo received lecture notes from courses which had been given at the Collegio Romano, for he made copies of such material which still survive today. The correspondence began around 1588 and continued for many years. Also in 1588 Galileo received a prestigious invitation to lecture on the dimensions and location of hell in Dante's Inferno at the Academy in Florence.

Fantoni left the chair of mathematics at the University of Pisa in 1589 and Galileo was appointed to fill the post (although this was only a nominal position to provide financial support for Galileo). Not only did he receive strong recommendations from Clavius, but he also had acquired an excellent reputation through his lectures at the Florence Academy in the previous year. The young mathematician had rapidly acquired the reputation that was necessary to gain such a position, but there were still higher positions at which he might aim. Galileo spent three years holding this post at the university of Pisa and during this time he wrote De Motu a series of essays on the theory of motion which he never published. It is likely that he never published this material because he was less than satisfied with it, and this is fair for despite containing some important steps forward, it also contained some incorrect ideas. Perhaps the most important new ideas which De Motu contains is that one can test theories by conducting experiments. In particular the work contains his important idea that one could test theories about falling bodies using an inclined plane to slow down the rate of descent.

In 1591 Vincenzo Galilei, Galileo's father, died and since Galileo was the eldest son he had to provide financial support for the rest of the family and in particular have the necessary financial means to provide dowries for his two younger sisters. Being professor of mathematics at Pisa was not well paid, so Galileo looked for a more lucrative post. With strong recommendations from Guidobaldo del Monte, Galileo was appointed professor of mathematics at the University of Padua (the university of the Republic of Venice) in 1592 at a salary of three times what he had received at Pisa. On 7 December 1592 he gave his inaugural lecture and began a period of eighteen years at the university, years which he later described as the happiest of his life. At Padua his duties were mainly to teach Euclid's geometry and standard (geocentric) astronomy to medical students, who would need to know some astronomy in order to make use of astrology in their medical practice. However, Galileo argued against Aristotle's view of astronomy and natural philosophy in three public lectures he gave in connection with the appearance of a New Star (now known as 'Kepler's supernova') in 1604. The belief at this time was that of Aristotle, namely that all changes in the heavens had to occur in the lunar region close to the Earth, the realm of the fixed stars being permanent. Galileo used parallax arguments to prove that the New Star could not be close to the Earth. In a personal letter written to Johannes Kepler in 1598, Galileo had stated that he was a Copernican (believer in the theories of Copernicus). However, no public sign of this belief was to appear until many years later.

At Padua, Galileo began a long term relationship with Maria Gamba, who was from Venice, but they did not marry perhaps because Galileo felt his financial situation was not good enough. In 1600 their first child Virginia was born, followed by a second daughter Livia in the following year. In 1606 their son Vincenzo was born.

We mentioned above an error in Galileo's theory of motion as he set it out in De Motu around 1590. He was quite mistaken in his belief that the force acting on a body was the relative difference between its specific gravity and that of the substance through which it moved. Galileo wrote to his friend Paolo Sarpi, a fine mathematician who was consultor to the Venetian government, in 1604 and it is clear from his letter that by this time he had realised his mistake. In fact he had returned to work on the theory of motion in 1602 and over the following two years, through his study of inclined planes and the pendulum, he had formulated the correct law of falling bodies and had worked out that a projectile follows a parabolic path. However, these famous results would not be published for another 35 years.

In May 1609, Galileo received a letter from Paolo Sarpi telling him about a spyglass that a Dutchman had shown in Venice. Galileo wrote in the Starry Messenger (Sidereus Nuncius) in April 1610:-

About ten months ago a report reached my ears that a certain Fleming had constructed a spyglass by means of which visible objects, though very distant from the eye of the observer, were distinctly seen as if nearby. Of this truly remarkable effect several experiences were related, to which some persons believed while other denied them. A few days later the report was confirmed by a letter I received from a Frenchman in Paris, Jacques Badovere, which caused me to apply myself wholeheartedly to investigate means by which I might arrive at the invention of a similar instrument. This I did soon afterwards, my basis being the doctrine of refraction.

From these reports, and using his own technical skills as a mathematician and as a craftsman, Galileo began to make a series of telescopes whose optical performance was much better than that of the Dutch instrument. His first telescope was made from available lenses and gave a magnification of about four times. To improve on this Galileo learned how to grind and polish his own lenses and by August 1609 he had an instrument with a magnification of around eight or nine. Galileo immediately saw the commercial and military applications of his telescope (which he called a perspicillum) for ships at sea. He kept Sarpi informed of his progress and Sarpi arranged a demonstration for the Venetian Senate. They were very impressed and, in return for a large increase in his salary, Galileo gave the sole rights for the manufacture of telescopes to the Venetian Senate. It seems a particularly good move on his part since he must have known that such rights were meaningless, particularly since he always acknowledged that the telescope was not his invention!

By the end of 1609 Galileo had turned his telescope on the night sky and began to make remarkable discoveries. Swerdlow writes (see [16]):-

In about two months, December and January, he made more discoveries that changed the world than anyone has ever made before or since.

The astronomical discoveries he made with his telescopes were described in a short book called the Starry Messenger published in Venice in May 1610. This work caused a sensation. Galileo claimed to have seen mountains on the Moon, to have proved the Milky Way was made up of tiny stars, and to have seen four small bodies orbiting Jupiter. These last, with an eye to getting a position in Florence, he quickly named 'the Medicean stars'. He had also sent Cosimo de Medici, the Grand Duke of Tuscany, an excellent telescope for himself.

The Venetian Senate, perhaps realising that the rights to manufacture telescopes that Galileo had given them were worthless, froze his salary. However he had succeeded in impressing Cosimo and, in June 1610, only a month after his famous little book was published, Galileo resigned his post at Padua and became Chief Mathematician at the University of Pisa (without any teaching duties) and 'Mathematician and Philosopher' to the Grand Duke of Tuscany. In 1611 he visited Rome where he was treated as a leading celebrity; the Collegio Romano put on a grand dinner with speeches to honour Galileo's remarkable discoveries. He was also made a member of the Accademia dei Lincei (in fact the sixth member) and this was an honour which was especially important to Galileo who signed himself 'Galileo Galilei Linceo' from this time on.

While in Rome, and after his return to Florence, Galileo continued to make observations with his telescope. Already in the Starry Messenger he had given rough periods of the four moons of Jupiter, but more precise calculations were certainly not easy since it was difficult to identify from an observation which moon was I, which was II, which III, and which IV. He made a long series of observations and was able to give accurate periods by 1612. At one stage in the calculations he became very puzzled since the data he had recorded seemed inconsistent, but he had forgotten to take into account the motion of the Earth round the sun.

Galileo first turned his telescope on Saturn on 25 July 1610 and it appeared as three bodies (his telescope was not good enough to show the rings but made them appear as lobes on either side of the planet). Continued observations were puzzling indeed to Galileo as the bodies on either side of Saturn vanished when the ring system was edge on. Also in 1610 he discovered that, when seen in the telescope, the planet Venus showed phases like those of the Moon, and therefore must orbit the Sun not the Earth. This did not enable one to decide between the Copernican system, in which everything goes round the Sun, and that proposed by Tycho Brahe in which everything but the Earth (and Moon) goes round the Sun which in turn goes round the Earth. Most astronomers of the time in fact favoured Brahe's system and indeed distinguishing between the two by experiment was beyond the instruments of the day. However, Galileo knew that all his discoveries were evidence for Copernicanism, although not a proof. In fact it was his theory of falling bodies which was the most significant in this respect, for opponents of a moving Earth argued that if the Earth rotated and a body was dropped from a tower it should fall behind the tower as the Earth rotated while it fell. Since this was not observed in practice this was taken as strong evidence that the Earth was stationary. However Galileo already knew that a body would fall in the observed manner on a rotating Earth.

Other observations made by Galileo included the observation of sunspots. He reported these in Discourse on floating bodies which he published in 1612 and more fully in Letters on the sunspots which appeared in 1613. In the following year his two daughters entered the Franciscan Convent of St Matthew outside Florence, Virginia taking the name Sister Maria Celeste and Livia the name Sister Arcangela. Since they had been born outside of marriage, Galileo believed that they themselves should never marry. Although Galileo put forward many revolutionary correct theories, he was not correct in all cases. In particular when three comets appeared in 1618 he became involved in a controversy regarding the nature of comets. He argued that they were close to the Earth and caused by optical refraction. A serious consequence of this unfortunate argument was that the Jesuits began to see Galileo as a dangerous opponent.

Despite his private support for Copernicanism, Galileo tried to avoid controversy by not making public statements on the issue. However he was drawn into the controversy through Castelli who had been appointed to the chair of mathematics in Pisa in 1613. Castelli had been a student of Galileo's and he was also a supporter of Copernicus. At a meeting in the Medici palace in Florence in December 1613 with the Grand Duke Cosimo II and his mother the Grand Duchess Christina of Lorraine, Castelli was asked to explain the apparent contradictions between the Copernican theory and Holy Scripture. Castelli defended the Copernican position vigorously and wrote to Galileo afterwards telling him how successful he had been in putting the arguments. Galileo, less convinced that Castelli had won the argument, wrote Letter to Castelli to him arguing that the Bible had to be interpreted in the light of what science had shown to be true. Galileo had several opponents in Florence and they made sure that a copy of the Letter to Castelli was sent to the Inquisition in Rome. However, after examining its contents they found little to which they could object.

The Catholic Church's most important figure at this time in dealing with interpretations of the Holy Scripture was Cardinal Robert Bellarmine. He seems at this time to have seen little reason for the Church to be concerned regarding the Copernican theory. The point at issue was whether Copernicus had simply put forward a mathematical theory which enabled the calculation of the positions of the heavenly bodies to be made more simply or whether he was proposing a physical reality. At this time Bellarmine viewed the theory as an elegant mathematical one which did not threaten the established Christian belief regarding the structure of the universe.

In 1616 Galileo wrote the Letter to the Grand Duchess which vigorously attacked the followers of Aristotle. In this work, which he addressed to the Grand Duchess Christina of Lorraine, he argued strongly for a non-literal interpretation of Holy Scripture when the literal interpretation would contradict facts about the physical world proved by mathematical science. In this Galileo stated quite clearly that for him the Copernican theory is not just a mathematical calculating tool, but is a physical reality:-

I hold that the Sun is located at the centre of the revolutions of the heavenly orbs and does not change place, and that the Earth rotates on itself and moves around it. Moreover ... I confirm this view not only by refuting Ptolemy's and Aristotle's arguments, but also by producing many for the other side, especially some pertaining to physical effects whose causes perhaps cannot be determined in any other way, and other astronomical discoveries; these discoveries clearly confute the Ptolemaic system, and they agree admirably with this other position and confirm it.

Pope Paul V ordered Bellarmine to have the Sacred Congregation of the Index decide on the Copernican theory. The cardinals of the Inquisition met on 24 February 1616 and took evidence from theological experts. They condemned the teachings of Copernicus, and Bellarmine conveyed their decision to Galileo who had not been personally involved in the trial. Galileo was forbidden to hold Copernican views but later events made him less concerned about this decision of the Inquisition. Most importantly Maffeo Barberini, who was an admirer of Galileo, was elected as Pope Urban VIII. This happened just as Galileo's book Il saggiatore (The Assayer) was about to be published by the Accademia dei Lincei in 1623 and Galileo was quick to dedicate this work to the new Pope. The work described Galileo's new scientific method and contains a famous quote regarding mathematics:-

Philosophy is written in this grand book, the universe, which stands continually open to our gaze. But the book cannot be understood unless one first learns to comprehend the language and read the characters in which it is written. It is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures without which it is humanly impossible to understand a single word of it; without these one is wandering in a dark labyrinth.

Pope Urban VIII invited Galileo to papal audiences on six occasions and led Galileo to believe that the Catholic Church would not make an issue of the Copernican theory. Galileo, therefore, decided to publish his views believing that he could do so without serious consequences from the Church. However by this stage in his life Galileo's health was poor with frequent bouts of severe illness and so even though he began to write his famous Dialogue in 1624 it took him six years to complete the work.

Galileo attempted to obtain permission from Rome to publish the Dialogue in 1630 but this did not prove easy. Eventually he received permission from Florence, and not Rome. In February 1632 Galileo published Dialogue Concerning the Two Chief Systems of the World - Ptolemaic and Copernican. It takes the form of a dialogue between Salviati, who argues for the Copernican system, and Simplicio who is an Aristotelian philosopher. The climax of the book is an argument by Salviati that the Earth moves which was based on Galileo's theory of the tides. Galileo's theory of the tides was entirely false despite being postulated after Johannes Kepler had already put forward the correct explanation. It was unfortunate, given the remarkable truths the Dialogue supported, that the argument which Galileo thought to give the strongest proof of Copernicus's theory should be incorrect.

Shortly after publication of Dialogue Concerning the Two Chief Systems of the World - Ptolemaic and Copernican the Inquisition banned its sale and ordered Galileo to appear in Rome before them. Illness prevented him from travelling to Rome until 1633. Galileo's accusation at the trial which followed was that he had breached the conditions laid down by the Inquisition in 1616. However a different version of this decision was produced at the trial rather than the one Galileo had been given at the time. The truth of the Copernican theory was not an issue therefore; it was taken as a fact at the trial that this theory was false. This was logical, of course, since the judgement of 1616 had declared it totally false.

Found guilty, Galileo was condemned to lifelong imprisonment, but the sentence was carried out somewhat sympathetically and it amounted to house arrest rather than a prison sentence. He was able to live first with the Archbishop of Siena, then later to return to his home in Arcetri, near Florence, but had to spend the rest of his life watched over by officers from the Inquisition. In 1634 he suffered a severe blow when his daughter Virginia, Sister Maria Celeste, died. She had been a great support to her father through his illnesses and Galileo was shattered and could not work for many months. When he did manage to restart work, he began to write Discourses and mathematical demonstrations concerning the two new sciences.

After Galileo had completed work on the Discourses it was smuggled out of Italy, and taken to Leyden in Holland where it was published. It was his most rigorous mathematical work which treated problems on impetus, moments, and centres of gravity. Much of this work went back to the unpublished ideas in De Motu from around 1590 and the improvements which he had worked out during 1602-1604. In the Discourses he developed his ideas of the inclined plane writing:-

I assume that the speed acquired by the same movable object over different inclinations of the plane are equal whenever the heights of those planes are equal.

He then described an experiment using a pendulum to verify his property of inclined planes and used these ideas to give a theorem on acceleration of bodies in free fall:-

The time in which a certain distance is traversed by an object moving under uniform acceleration from rest is equal to the time in which the same distance would be traversed by the same movable object moving at a uniform speed of one half the maximum and final speed of the previous uniformly accelerated motion.

After giving further results of this type he gives his famous result that the distance that a body moves from rest under uniform acceleration is proportional to the square of the time taken.

One would expect that Galileo's understanding of the pendulum, which he had since he was a young man, would have led him to design a pendulum clock. In fact he only seems to have thought of this possibility near the end of his life and around 1640 he did design the first pendulum clock. Galileo died in early 1642 but the significance of his clock design was certainly realised by his son Vincenzo who tried to make a clock to Galileo's plan, but failed.

It was a sad end for so great a man to die condemned of heresy. His will indicated that he wished to be buried beside his father in the family tomb in the Basilica of Santa Croce but his relatives feared, quite rightly, that this would provoke opposition from the Church. His body was concealed and only placed in a fine tomb in the church in 1737 by the civil authorities against the wishes of many in the Church. On 31 October 1992, 350 years after Galileo's death, Pope John Paul II gave an address on behalf of the Catholic Church in which he admitted that errors had been made by the theological advisors in the case of Galileo. He declared the Galileo case closed, but he did not admit that the Church was wrong to convict Galileo on a charge of heresy because of his belief that the Earth rotates round the sun.

Article by: J J O'Connor and E F Robertson

Read More